CUBE GAMES
Written & Designed By William F. BultasIllustrated By Darryl T. Miyaguchi
Required Equipment: A sheet of paper, pen or pencil, & a coin or die. Though not required, a RUBIK'S Cube could be a useful visual aid.
Instructions: There are 4 cube games, all based upon the figures shown. All 4 games are suitable for 2 players & can be conducted in person or by correspondence. You may print out, copy, & distribute these rules.
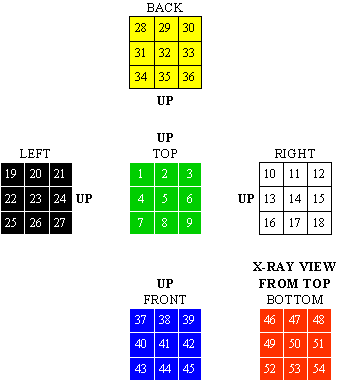
The following 6 3x3 grids each denote a side of the cube illustrated above. UP is written by each grid to show its orientation if you are looking down at the cube. A number is written on each of the squares of each face of the cube. This allows you to tell your opponent exactly where you are moving on the cube in each of the following games. Each time that you make a move, you simply write the number of the square(s) that you have moved to, & then your opponent does the same, & so on, until one of you wins. Record keeping may be made easier by writing the number for each square, & marking each off as it is moved to; this aids in avoiding duplication. Randomly determine which player begins each game. If a game has already been played, the loser of the last game moves first.
This is a variation of a very well known & simple game. One player marks an 'X' each turn, while the other uses an 'O' during his or her turn. But instead of actually writing these symbols on the cube, you may simply write the number for the space on which your mark is to appear. The object is to get 4 of the same mark in a row vertically or horizontally (diagonally doesn't count). If a player accomplishes this, he or she wins. Obviously, it is necessary to have the marks on 2 different sides to have 4 in a row, so one must view these marks as 'wrapping around' the cube.
Imagine that the cube is floating in space, & has sugar on each of its 54 squares. Each player is Adam or Army, 2 ants trying to eat as much sugar as possible. Each turn, a player randomly determines if he or she will move 1 or 2 spaces. If it is determined that it will be 2 spaces, the player cannot choose to move only 1 space. During each player's first turn, he or she may choose to 'land' on any square on the cube that has not previously been occupied. This is the player's first move. Each ant may move to any square on the cube that shares a side or corner with the square that the ant currently occupies. However, neither ant may ever move to a square that has previously been occupied by either ant. The game ends when an ant must move, but cannot move to any square that has not already been occupied. When this happens, the other player wins.
If you don't like the name of this game, you can call it Cubic Roulette. The scenario & rules for Hungry Ants apply in their entirety, but in this game the ants are far less coordinated, thus making each movement less predictable. For every move made, including the very first one, each player must choose 2 squares that he or she would like to land on; the player must be able to actually reach either of the squares without breaking the rules, & if there is only 1 square available that could be moved to, this step can be skipped. The player must randomly determine which of the 2 squares he or she will actually move to for each move that is made. The winner is declared when the opposing ant must move, but cannot move to any square that has not already been occupied.
In the year 2119, 2 space ships representing the Bluesuit & Redsuit rival corporations arrive on a small planet that contains a high concentration of an extremely valuable mineral. Strangely enough, the planet happens to be shaped like a cube. Each player takes on the role of a mining team for 1 of the corporations. The teams move about the planet mining the mineral, Cubazium, & do not leave each area entered until they have obtained all of the Cubazium present. The rules are the same as for Hungry Ants, but with the following exceptions: The objective of the game is to acquire as many points as possible; players may enter squares that have previously been or are currently occupied; each player earns 1 point for each previously unoccupied square that he or she lands on; the game ends when all squares have been occupied at least once, & the player with the most points is then declared the winner.
Have fun!